2024. 2. 10. 11:11ㆍCS - Roadmap.sh/3. Common Algorithms
CS - 3. Common Algorithms - 3.8 Back Tracking Algorithm - 3.8.2 Solving n Queen Problem
Solving n Queen Problem
N Queen Problem is a famous problem in Computer Science. It is a problem of placing n queens on an n x n chessboard such that no two queens attack each other. The problem is to find all possible solutions to the problem.
N 여왕 문제는 컴퓨터 과학에서 유명한 문제입니다. 두 여왕이 서로 공격하지 않도록 n x n 체스판 위에 n개의 여왕을 배치하는 문제입니다. 문제는 문제에 대한 가능한 모든 해결책을 찾는 것입니다.
N-Queen 문제?
N-Queen 문제는 체스판 위에 N개의 퀸을 배치하는 문제로써, 모든 퀸이 서로를 공격할 수 없도록 배치하는 것이 목표입니다. 즉, 모든 퀸이 같은 행, 열, 또는 대각선에 위치하지 않아야합니다.
In Python
def is_safe(board, row, col, n):
# 이 위치에 퀸을 놓을 수 있는지 확인하는 함수
for i in range(col):
if board[row][i] == 1:
return False
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
for i, j in zip(range(row, n, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solve_n_queen(board, col, n):
# 모든 퀸을 배치하면 True를 반환
if col >= n:
return True
# 각 행에 퀸을 놓아보고, 놓을 수 있으면 놓고 다음 열로 넘어감
for i in range(n):
if is_safe(board, i, col, n):
board[i][col] = 1
if solve_n_queen(board, col + 1, n):
return True
board[i][col] = 0 # 퀸을 놓을 수 없다면 이 위치에 놓지 않고 다음 행으로 이동
return False # 이 열에 퀸을 놓을 수 있는 위치가 없다면 False 반환
def solve(n):
board = [[0]*n for _ in range(n)]
if not solve_n_queen(board, 0, n):
print("해결책이 없습니다.")
return
for i in board:
print(i)
return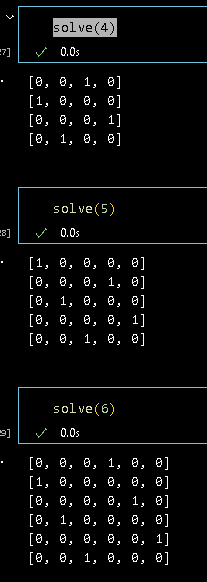

이것은 하나의 해결방안이고 여러가지 해결방법이 있을 수 있다.
사족
계속 보다보면 뭔가 떠오르는 것이 있다.
오목할 때의 필승법인... 日(날 일) ..
N-Queen 은 오목과의 연관성이..?
참고
https://www.acmicpc.net/problem/9663 백준 N-Queen 9663
'CS - Roadmap.sh > 3. Common Algorithms' 카테고리의 다른 글
| Knight’s Tour Problem(임시_) (1) | 2024.02.12 |
|---|---|
| Maze Solving Problem(임시) (0) | 2024.02.11 |
| 3.8 Back Tracking Algorithm(역추적 알고리즘) - 3.8.1 Finding Hamiltonian Paths(해밀턴 경로) (2) | 2024.02.10 |
| 3.7.3 Post-Order Traversal (1) | 2024.02.10 |
| 3.7.2 In-Order Traversal(중위 순회) (0) | 2024.02.09 |