2024. 1. 3. 20:10ㆍCS - Roadmap.sh/1. Data structures
Data structures (with python) - 2. Graph - 2.3. Spanning Tree
Spanning Tree
💡 A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..
스패닝 트리는 그래프 G의 하위 집합으로, 모든 정점이 가능한 최소 수의 에지로 덮여 있습니다. 따라서 스패닝 트리에는 주기가 없으며 연결이 끊어질 수 없습니다.
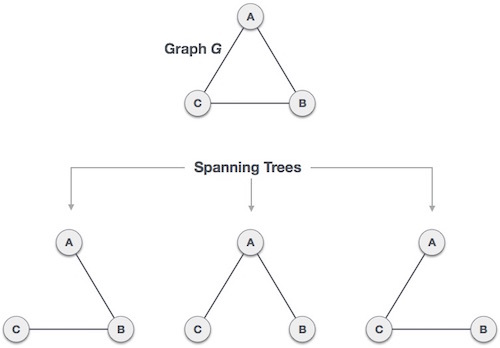
Spanning Tree 는 뒤에 Tree 라고 붙지만 구지 분류하자면 Tree보다 graph theory의 중요 개념에 속한다.
앞서 그래프 이론은, 노드(node)와 그사이를 연결하는 엣지(edge)의 집합으로 이루어진 그래프를 연구한다.
스패닝 트리는 그래프의 서브그래프(subgraph)이며,
그래프의 트리 구조를 나타내주기 때문에 그래프 이론의 일부로 분류된다.
(Tree 이론에는 - binary, binary search, full binary, complete binary, balanced, unbalanced Tree 들이 있다.
이 시리즈에서 정리할 tree들 이다.)
최소 스패닝 트리 알고리즘에는
kruskal과 prim 알고리즘이 있다.
Kruskal 알고리즘을 파이썬에서 구현해보자
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = []
# 그래프를 초기화한다.
# vertices는 그래프의 정점의 수
# self.graph 그래프의 간선을 저장하는 리스트
def add_edge(self, u, v, w):
self.graph.append([u, v, w])
# u, v 는 간선의 양 끝 정점
# w는 간선의 가중치
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
#fine(self, parent, i)이 메서드에서 부모배열의 i 번째 정점의 루투를 찾는다.
def union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
else :
parent[yroot] = xroot
rank[xroot] += 1
# union 메서드는 두 개의 서로 다른 집합을 합친다.
# x, y는 각각 집합을 대표하는 루트 정점
# 이 메서드에서 두 집합의 rank를 비교해 랭크가 더 낮은 집합을 랭크가 더 높은 집합에 합친다.
# 랭크가 같은 경우에는 한 집합을 다른 집합에 합치고 랭크를 1 증가시킨다.
def kruskal(self):
result = []
i = 0
e = 0
self.graph = sorted(self.graph, key=lambda item: item[2])
parent = []
rank = []
for node in range(self.V):
parent.append(node)
rank.append(0)
while e < self.V - 1:
u, v, w = self.graph[i]
i += 1
x = self.find(parent, u)
y = self.find(parent, v)
if x != y:
e += 1
result.append([u, v, w])
self.union(parent, rank, x, y)
return result
# kruskal 이 메서드는 크루스칼 알고리즘을 실행, 최소 스패닝 트리를 찾는다.
# 간선들을 가중치의 오름차순으로 정렬하고(sorted),
# 가장 가중치가 작은 간선부터 선택하여 스패닝 트리에 추가한다.
# 간선을 추가할 때에 해당 간선이 사이클을 형성하는지 확인하고,
# 사이클을 형성하지 않는 경우에만 스패닝 트리에 추가한다
이해하기 쉽게 클래스의 각 메서드 마다 주석을 달아놓았다.
g = Graph(4)
g.add_edge(0, 1, 10)
g.add_edge(0, 2, 6)
g.add_edge(0, 3, 5)
g.add_edge(1, 3, 15)
g.add_edge(2, 3, 4)
print(g.kruskal()) # [[2, 3, 4], [0, 3, 5], [0, 1, 10]]위 코드는 4개의 노드와 5개의 간선을 가진 그래프에서 스패닝 트리를 찾는다.
결과는 선택된 간선들과 각 간선의 가중치를 나타낸다.
(추후 그림설명 추가)
4개의 노드 (0123), 5 개의 간선 (0-1, 0-2, 0-3, 1-3, 2-3) 으로 생성한다.
각 가중치 (10,6,5,15,4)
크루스칼 알고리즘은 가장 가중치가 작은 간선부터 선택한다.
1. 가중치4 인 간선 2-3 선택. -> [[2,3,4]]
2. 차례대로 가중치 5인 0-3
[[2,3,4], [0,3,5]]
3. 그다음 가중치 6인 간선 0-2를 선택하고 추가하면
사이클 0-2-3-0 이 형성되어 버려 스패닝 트리가 아니다.
4. 그다음 가중치 10 , 0-1을 선택하면 사이클이 형성되지 않으므로 스패닝 트리에 추가한다.
[[2,3,4],[0,3,5],[0,1,10]]
5. 마지막 가중치 15, 1-3 은
이미 0-1, 0-3 간선이 선택되어있다.
따라서 1-3 간선을 추가하면 1-0-3-1 이런 사이클이 형성 된다.
따라서 스패닝 트리에 추가되지 않는다.
최종적인 최소 스패닝 트리는 2-3, 0-3, 0-1로 이루어져 있는
[[2,3,4],[0,3,5],[0,1,10]]이 된다.
정리
스패닝 트리 (Spanning tree)는
1. cycle(loop)가 없다.
2. 모든 정점이 가능한 최소 수의 에지로 덮여있다.
활용
1. 네트워크 계획
2. 컴퓨터 네트워크 라우팅 프로토콜
3. 클러스터 분석
'CS - Roadmap.sh > 1. Data structures' 카테고리의 다른 글
| Data structures (with python) - 3. Heap (0) | 2024.01.05 |
|---|---|
| Data structures (with python) - 2. Graph - 2.4. Graph Representation (1) | 2024.01.04 |
| Data structures (with python) - 2. Graph - 2.2. Undirected graph (0) | 2024.01.02 |
| Data structures (with python) - 2. Graph - 2.1. Directed graph (0) | 2024.01.01 |
| Data structures (with python) - 1. Array (0) | 2024.01.01 |